A ameaça por COVID-19 que o mundo enfrenta, e que se tornou realidade em Portugal no início do mês de Março, tem feito parte do quotidiano e tem dominado notícias e conversas. De um momento para o outro, passámos a ouvir expressões como crescimento exponencial, curvas de crescimento, ponto de inflexão, modelos SIR e muitas outras expressões de cariz matemático. Para a grande maioria das pessoas, estas expressões pouco dizem e pouco importam e as atenções viram-se para o número diário de novos infectados e a percentagem de variação face ao dia anterior.
Quando, em determinado dia, se calcula a percentagem de aumento no número de infectados face ao dia anterior, ficamos a conhecer que peso representa a diferença entre o número de infectados nesses dois dias, em relação ao total verificado no dia anterior. Interessando saber como evoluíram essas diferenças em períodos maiores, por exemplo uma semana, é necessário considerar as várias percentagens de aumento, de dia para dia, e usar essa informação na sua globalidade.
Perante um conjunto de valores, a necessidade de resumir a informação nele contida e sintetizá-la num valor representativo desse conjunto passa, frequentemente, pela determinação de medidas que traduzam o centro da distribuição dos valores, que são denominadas medidas de tendência central.
A mais comum das medidas de tendência central é a média aritmética que, quer seja simples ou ponderada, se adequa a inúmeras situações. Talvez pelo seu uso tão generalizado, talvez pelo desconhecimento da sua desadequação em determinados casos, a média aritmética é adoptada, muitas vezes, em situações em que a sua aplicação não é válida e o seu valor não tem sentido. Uma dessas situações, encontrada numa notícia online de um meio de comunicação social de âmbito nacional, onde era referida a variação média no número de infectados por COVID-19, em Portugal, numa semana, serviu de mote para este texto.
A média aritmética
Para determinar a média aritmética, de um conjunto de valores, calcula-se o quociente entre a soma de todos esses valores e o número total de valores. Recorrendo à simbologia matemática, para um conjunto de n valores positivos, a média aritmética é dada por
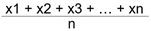
A média aritmética preserva a soma dos valores do conjunto, o que significa que se substituirmos cada valor x1, x2, x3, …, xn pelo valor da média (MA), temos
x1 + x2 + x3 + … + xn = MA + MA + MA + … + MA (MA adicionado n vezes)
Assim, o princípio por detrás da média aritmética é o de divisão equitativa, ou seja, calculando a média aritmética de um conjunto de valores obtemos o valor que seria observado se todos esses valores fossem iguais.
A média aritmética é uma medida razoavelmente estável, não sendo muito afectada quando alguns (poucos) dos valores envolvidos são moderadamente grandes ou moderadamente pequenos, relativamente aos restantes, verificando-se que esta estabilidade aumenta quanto maior for o número total de valores envolvidos. A existência de um ou mais valores extremos (marcadamente distantes dos restantes) afecta bastante o valor da média, e influencia negativamente a sua utilidade e validade. Nesses casos é necessário recorrer à mediana ou à moda que, sendo também medidas de tendência central, são uma boa alternativa à média aritmética por não serem influenciadas por valores extremos.
A média geométrica
A média geométrica é outra medida de tendência central, de aplicação menos frequente que média aritmética, mediana ou moda, mas imprescindível em situações em que o conjunto de valores observados é constituído por taxas ou percentagens, situações que são comuns nas áreas da Matemática Financeira, Bacteriologia ou Demografia.
Para um conjunto de n valores positivos, x1, x2, x3, …, xn, a média geométrica é a raiz de ordem n do produto dos n valores, ou, em simbologia matemática

A média geométrica preserva o produto dos valores, isto é, se substituirmos cada valor x1, x2, x3, …, xn, pelo valor da média geométrica (MG), temos
x1 × x2 × x3 × … × xn = MG × MG × MG × … × MG (MG multiplicado n vezes)
Exemplo
Para ilustrar a diferença entre média aritmética e média geométrica, e a desadequação da média aritmética em situações em que os valores envolvidos são taxas (razões/percentagens), consideremos a seguinte situação, hipotética, em que se conhece o número de habitantes de uma cidade e a taxa de crescimento anual dessa população.
Suponhamos que a população no início de determinado ano, que consideramos o ano 1, é de 10000 habitantes, que nesse ano a população teve um crescimento de 5% e que nos dois anos seguintes a população cresceu 10% e 12%. Pretendemos saber a que taxa média cresceu a população nesses três anos.
Na Tabela 1 são apresentados os valores iniciais e finais da população em cada um dos anos.

Se calcularmos a média aritmética dos factores de crescimento, obtemos:
(1,05 + 1,1 + 1,12) / 3 = 1,09
Portanto, a taxa média seria de 9%.
Como vimos, a média aritmética preserva a soma dos valores do conjunto. Então, se a média aritmética fosse adequada para esta situação, substituindo cada factor de crescimento anual pela média (aritmética), a população no final do 3º ano teria de ser igual à indicada na Tabela 1. Como se pode ver a seguir, na Tabela 2, tal não se verifica.

E o que aconteceria se adoptássemos a média geométrica?
A média geométrica dos três factores de crescimento é a raiz cúbica do seu produto:
Substituindo, agora, cada factor de crescimento anual pela média geométrica podemos verificar que o valor da população, ao final dos três anos, é o correcto (tabela 3).
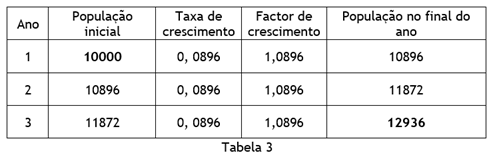
Nota: Na notícia, que serviu de mote para este texto, publicada em 3 de Abril, é indicado que a variação média no número de infectados por COVID-19, em Portugal, na referida semana, foi de 15,7%. Recorrendo aos valores disponibilizados pela DGS, verifica-se que esse é o valor da média aritmética. Como vimos a média aritmética não é adequada quando os valores envolvidos são taxas (razões/percentagens). Em rigor, a variação média no número de infectados por COVID-19, em Portugal, na referida semana, foi de 15,58%, que corresponde à média geométrica das taxas de crescimento diárias (factores de crescimento diários).