AINDA NOS RESTA UM TEMPINHO ATÉ AO FIM DO MUNDO

A Torre de Hanói é um passatempo que foi criado pelo matemático francês Edouard Lucas, em 1883. Na sua forma original, publicada na obra Récréations mathematiques  (1882-1894), a Torre de Hanói consistia em três pinos fixados num suporte e 8 discos de diferentes diâmetros, inicialmente dispostos num dos pinos, por ordem decrescente do seu diâmetro, formando uma torre de forma aproximadamente cónica.

O objectivo do jogo é deslocar todos os discos, do pino onde se encontram, para um dos pinos vazios (normalmente o da direita), de forma a formar uma torre igual à inicial, movendo um disco de cada vez, não sendo permitido colocar um disco maior sobre um disco menor, mas podendo usar o pino excedente para movimento intermédios.

Nas instruções, que acompanhavam a versão original do jogo, Lucas incluía uma breve referência a uma lenda indiana, sobre os três templos da cidade de Benares, que é considerada a cidade mais antiga do mundo. Um ano mais tarde, num artigo da revista Nature, Henri Parville reinventa a lenda, dando-lhe a forma poética que desde então se associa à Torre de Hanói:

“No grande templo de Benares, debaixo da cúpula que marcava o centro do mundo existia uma placa de bronze com três hastes de diamantes, cada uma de um palmo de altura e da grossura do corpo de uma abelha. Numa dessas hastes, Deus, no momento da criação do mundo, colocou 64 discos de ouro, o maior sobre a base de bronze e os restantes por cima deste, por ordem decrescente dos diâmetros. Deus chamou os seus sacerdotes e ordenou-lhe que transferissem incessantemente, dia e noite, os discos da haste inicial para outra, de acordo com as leis fixas e imutáveis do bramanismo, que exigiam que nunca se movesse mais de um disco por vez e nunca se colocasse um disco maior sobre um menor. Quando todos os 64 discos forem transferidos para a outra haste, a torre e o templo serão transformados em pó e o mundo desaparecerá.”

O passatempo da torre de Hanói, actualmente conhecido também como “Torres de Brahama” ou “Problema do fim do mundo” seria, portanto, uma variante da tarefa encomendada por Deus aos seus sacerdotes.

De acordo com esta lenda quando chegará o fim do mundo?

Para encontrar a resposta à questão anterior, iremos partir do caso mais elementar de uma torre de Hanói (uma torre com apenas um disco) percorrendo versões progressivamente mais complexas, encontrando o número mínimo de movimentos necessários à conclusão do jogo.

Com apenas um disco, bastará, obviamente, um único movimento para o transferir para outra haste.

Se a torre for formada por dois discos será necessário realizar três movimentos. Designemos as hastes por A, B e C. O primeiro movimento consiste em colocar o disco menor na haste B, em seguida, passar o disco maior para a haste C e, finalmente, colocar o disco menor sobre o disco maior, como ilustrado na imagem seguinte.

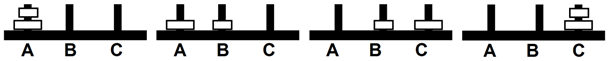
Com três discos, necessitaremos de 7 movimentos, procedendo da seguinte forma: passar, sucessivamente, os dois discos menores para a haste B. Para mudar dois discos de haste são necessários, como já sabemos, 3 movimentos.

O disco maior pode agora passar para a haste C.

Para colocar os dois discos menores sobre o disco maior serão necessários, mais três movimentos.

Com 4 discos serão necessários 15 movimentos. Para colocar os três discos menores na haste B são necessários 7 movimentos. Assim o disco maior fica livre e pode ser mudado para a haste C. Para transferir, para a haste C, os três discos que se encontram na haste B são necessários novamente 7 movimentos.

A tabela seguinte apresenta um resumo dos cálculos que descrevemos anteriormente para determinar o número mínimo de movimentos para concluir o jogo da Torre de Hanói, nos casos em que a torre tem 1, 2 3 ou 4 discos.

Da observação desta tabela, facilmente se verifica que:

·         Para uma torre com apenas 1 disco, o número mínimo de movimentos é  1 = 2¹ -1

·         Para uma torre com 2 discos, o número mínimo de movimentos é 3 = 2² - 1

·         Para uma torre com 3 discos, o número mínimo de movimentos é 7 = 2³ - 1

·         Para uma torre com 4 discos, o número mínimo de movimentos é 15 = 2⁴ - 1

Então para completar o jogo da Torre de Hanói, na sua versão de 8 discos, serão necessários, no mínimo, 2⁸ – 1 = 255 movimentos. E para qualquer número n de discos, o número mínimo de movimentos será 2ⁿ – 1.

Assim, de acordo com a lenda, o fim do mundo ocorreria quando os sacerdotes tivessem completado os 2⁶⁴ – 1 = 18.446.744.073.709.551.615 movimentos necessários para transferir os 64 discos de ouro para a outra haste.

Assumindo que cada movimento demoraria 1 segundo, decorreriam 18.446.744.073.709.551.615 segundos desde a criação do mundo até a sua extinção, ou seja, 213503982334601 dias, o que corresponde a cerca de 585 mil milhões de anos.

A acreditar na teoria que defende que o começo do Universo foi há cerca de 14 mil milhões de anos, ainda nos resta um tempinho, cerca de 571 mil milhões de anos, até ao fim do Mundo.

Imagem de lojadabia.com.br