Karl Friedrich Gauss, nascido em Brunswick, (Alemanha) em 30 de Abril de 1777 e falecido a 23 de Fevereiro de 1855, em Göttingen, Hannover (Alemanha), foi um dos maiores matemáticos de todos os tempos. A sua prodigiosa capacidade para a Matemática e o valor inestimável da sua contribuição em áreas como a Teoria dos Números, a Estatística, a Astronomia, a Geometria, a Análise, o Magnetismo e outras valeram-lhe, ainda em vida, ser apelidado de “Príncipe dos Matemáticos”.
Filho de uma família humilde, Gauss parecia estar destinado a seguir as pisadas de seu pai e de seu avô como jardineiro, mas a revelação, desde muito cedo, de capacidades intelectuais fora do comum levou a que a convicção da mãe, de que o filho deveria ter uma educação adequada, se sobrepusesse à vontade do pai.
O primeiro episódio que fazia adivinhar o talento de Gauss terá ocorrido quando Gauss tinha apenas 3 anos, e permite-nos perceber porque Gauss costumava dizer que tinha aprendido a contar antes de aprender a ler. Certo dia, estava o pai de Gauss prestes a pagar o salário a um dos trabalhadores que o auxiliava, quando o pequeno Gauss, que se encontrava por perto, exclamou "Papá, cometeste um erro!", indicando imediatamente o valor certo. Para espanto dos presentes, feita a confirmação, verificou-se que os cálculos que Gauss tinha feito mentalmente estavam correctos.
Antes de completar os sete anos, Gauss iniciou o ensino primário na velha escola de St. Katherinen Volkschule, onde pertencia a uma turma de mais de uma centena de alunos a cargo do Professor J.G. Büttner. Reza a história que, teria Gauss aproximadamente 8 anos, quando o professor, que considerava todos os alunos como incapazes e pouco dotados, descobriu que pouco mais teria para ensinar a Gauss. Sempre que o comportamento da turma não agradava ao professor Büttner, este propunha aos alunos tarefas demoradas que lhes exigissem uma boa dose de concentração e paciência. Nesse dia a tarefa consistia em determinar a soma dos números (naturais) de 1 até 100. Todos os alunos pegaram na sua ardósia executando a árdua tarefa de adicionar todas aquelas parcelas para a qual a ardósia parecia ser demasiado pequena. Todos menos Gauss!
Como era hábito nestas situações, à medida que os alunos terminavam a tarefa iam colocando as suas ardósias na secretária do professor. Qual não foi o espanto do professor quando Gauss se levantou para entregar a sua resposta, ainda os colegas mal tinham iniciado a tarefa. Gauss dirigiu-se ao professor e disse, no seu dialecto Braunschweig: "Ligget se" (Aqui está!), ao mesmo tempo que, sobre a secretária, colocava a sua ardósia onde apenas estava escrito um número de quatro algarismos, 5050.
Para chegar com tal rapidez à resposta, Gauss usou um método indirecto de cálculo ao observar que a soma do primeiro número (1) com o último número (100) é 101, do segundo número (2) com o penúltimo (99) é também 101, assim como para os outros pares de números que se seguem. Como a soma 101 se verifica para todos os cinquenta pares de números de 1 a 100, Gauss limitou-se a multiplicar 50 vezes 101, obtendo 5050. Na figura 1 é possível visualizar o raciocínio de Gauss que lhe permitiu abreviar os cálculos.
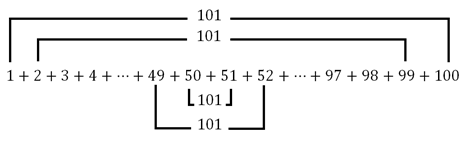
Figura 1: De 1 a 100 existem 50 pares de números cuja soma é 101.
Gauss tinha descoberto um método para determinar a soma dos termos de uma progressão aritmética finita!
Uma progressão aritmética é uma sucessão de números em que a diferença entre dois números consecutivos é sempre um valor constante (designado por razão da progressão).
A sequência numérica:
7 10 13 16 19 22 25 28
é uma progressão aritmética de razão 3 (a diferença entre dois termos consecutivos é sempre igual a 3) com primeiro termo 7 e último termo 28.
Apesar de a soma realizada por Gauss ser um caso particular de soma dos termos de uma progressão aritmética, (os números naturais de 1 até 100, constituem uma progressão aritmética de razão 1, com primeiro termo 1 e último termo 100) o método por ele usado pode ser aplicado em qualquer outra progressão aritmética.
Se aplicarmos o método de Gauss à sequência anterior, verifica-se que
|
7 |
+ |
28 |
= |
35 |
|
10 |
+ |
25 |
= |
35 |
|
13 |
+ |
22 |
= |
35 |
|
16 |
+ |
19 |
= |
35 |
ou seja, temos 4 pares cuja soma é 35, então
7 + 10 + 13 + 16 + 19 + 22 + 15 + 28 = 35 x 4 = 140.
Gauss descobriu que para obter a soma dos termos de uma qualquer progressão aritmética basta adicionar o primeiro e último termos e multiplicar por metade da quantidade dos termos dessa progressão aritmética
A soma dos termos da progressão aritmética
7 10 13 16 19 22 25 28
é ( 7 + 28 ) x 8 : 2 = ( 7 +28 ) x 4
A soma dos termos da progressão aritmética
1 2 3 … 97 98 99 10
é ( 1 + 100 ) x 100 : 2 = ( 1 + 100 ) x 50
Se designarmos por a1 o primeiro termo de uma progressão aritmética, por an o seu último termo e por n o número de termos que a constituem essa progressão aritmética, a soma (S) de todos os termos da progressão aritmética pode ser obtida através da fórmula
S = (a1 + na ) x n : 2
Talvez tenha reparado que ambas as progressões aritméticas apresentadas acima têm um número par de termos, mas este método funciona para todas as progressões aritméticas! Experimente com progressões aritméticas com um número impar de termos, por exemplo:
4 8 12 16 20 24 28 32 36
Imagem de wikimedia.org